Página 27 até 33
SISTEMA OCTAL
O sistema octal é composto por 8 (oito) valores, ou seja, “0, 1, 2, 3, 4, 5, 6, 7”. Pra converter o sistema octal para binário, a regra é a seguinte: separe os números em octal e verifique os seus valores coluna dos valores em binário (quadro anterior), lembrando que teremos que ter 3 (três) dígitos em cada valor binário.
Exemplo: Converteremos o número octal 4402 para binário. No quadro o número 4 em octal representa o 100 binário, o 0 representa o 0 binário (iremos acrescentar mais dois dígitos para ficar com três) que ficará 000 e o 2 representa o 10 binário que ficará 010. O Resultado da conversão será o valor em binário: 100100000010.
Conversão de binário para decimal. Para isso, seguiremos a mesma ideia que aprendemos na conversão de binário para decimal, ou seja, devemos pegar cada um dos algarismos que compõem nosso número octal e multiplicá-los pela base 8 (octal) elevado ao expoente 0, 1, 2, 3 e assim sucessivamente conforme a quantidade de algarismos que temos.
Representação de como efetuar a conversão da base octal para decimal
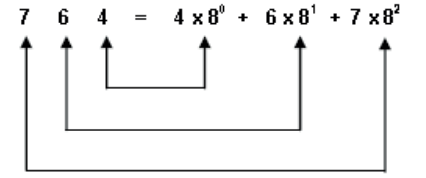
Agora fazemos a adição entre todos os resultados obtidos, que teríamos (4 x 80) + (6 x 81) + (7 x 82), que é igual a 4 + 48 + 448 que totaliza 500. Então podemos afirmar que o número octal 764 representa o número 500 em decimal.
Conversão de octal para hexadecimal. Para isso, precisaremos de duas regras. A primeira regra será pegar cada número octal e transformá-lo em número binário como visto anteriormente em grupos de 3 (três) dígitos. Depois dessa conversão, faz-se necessário agrupar os números binários em grupos de 4 (quatro) algarismos da direita para a esquerda. A cada grupo observa-se o seu valor correspondente em hexadecimal no quadro.
Exemplo: Converter o número octal 1057 para hexadecimal. Primeiramente separar cada número e encontrar o seu correspondente binário no quadro de conversão, lembrando que neste momento devemos ter 3 (três) dígitos binários. O número 1 em octal está representado por 1 em binário onde serão acrescidos mais 2 (dois) dígitos para completar os 3 (três) dígitos necessários ficando 001. O número 0 em octal é representado pelo 000 em binário já acrescido os outros dois dígitos. O número 5 em octal representa o número 101 (não é necessário acrescentar mais dígitos pois já possui os 3 requeridos) e o número 7 em octal representa o número 111. Teremos o valor 001000101111 como representação binária do número 1057 octal. O próximo passo será separar este valor em binário em grupos de 4 dígitos da direita para a esquerda, ou seja, 0010 0010 1111. De posse deste grupo de valores, basta olhar no quadro de conversão (Quadro) para verificar os valores correspondentes em hexadecimal. O número 0010 representa o número 2 em hexadecimal, o número 1111 representa o F então o número resultante dessa conversão será 2 2 F em hexadecimal.
SISTEMA DECIMAL
A conversão de um número decimal para binário envolve divisões sucessivas do decimal por 2.
Como exemplo, iremos converter o número decimal 1985 em binário. O procedimento deve ser o seguinte: dividir o número decimal por 2. Caso o resultado seja exato, aquela divisão terá resto 0 (zero), se não for exato terá resto 1 (um). Esse valor deve ser anotado da direita para a esquerda ou como mostrado no quadro. Deve-se dividir o número até que o quociente da divisão seja igual a 0 (zero).
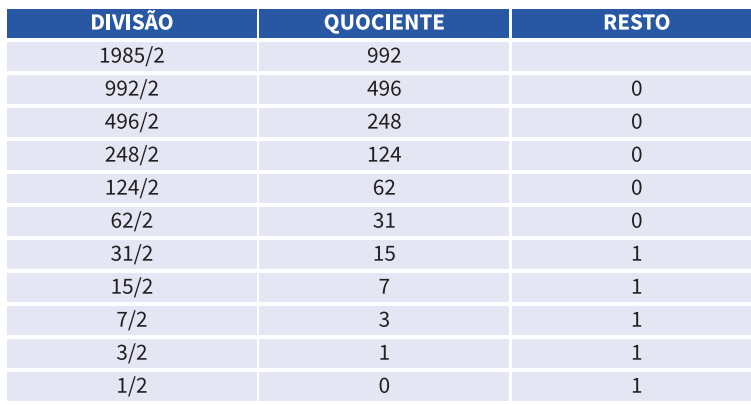
O resultado obtido é juntar o resultado de baixo para cima, onde o resultado é o seguinte número binário: 11111000001.
SISTEMA HEXADECIMAL E PREFIXOS BINÁRIOS
O sistema hexadecimal possui dezesseis representações sendo elas: “0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F”. De todos os sistemas numéricos apresentados nesta unidade para representar os dados, o sistema hexadecimal é o que apresenta o maior número de recursos. Neste sistema os numerais de 10 a 15 são representados por letras. Assim a letra A = 10, B = 11, C = 12, D = 13, E =14 e F = 15.
Conversão de base hexadecimal em base binária. Para converter um valor hexadecimal em um número binário, é necessário pegar cada um dos algarismos que fazem parte do valor hexadecimal e fazer a conversão individualmente.
O exemplo mostra o número hexadecimal A57F. Para converter basta separar cada número hexadecimal e verificar no quadro anterior qual o valor em binário correspondente. Assim, o número hexa A é igual a 1010 em binário, o número 5 é igual a 0101 (era 101 e foi incluído o 0 para ficar com 4 dígitos), o número 7 é igual a 0111 (era 111 e foi incluído o 0 para ficar com 4
dígitos) e o número F é igual a 1111 em binário. Então o valor em binário do número hexadecimal A57F é 1010010101111111.
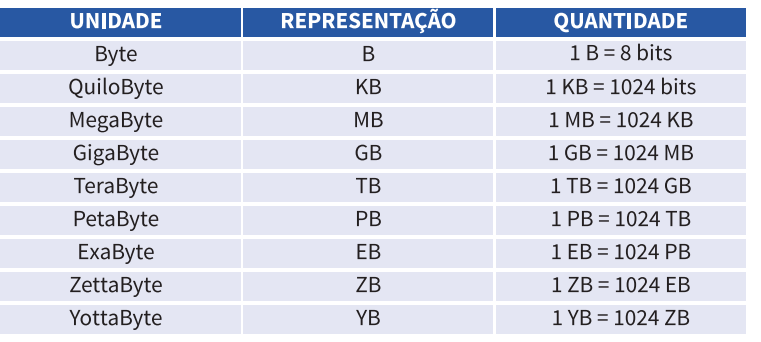
É comum utilizar os chamados prefixos binários para organizar as quantidades de bits de alguma informação. Os prefixos binários abreviam a forma de escrever as quantidades de bits e Bytes, sendo bastante úteis quando lidamos com uma quantidade muito alta.
O quadro a seguir apresenta alguns dos prefixos binários que podem ser utilizados, com suas respectivas representações e quantidades equivalentes